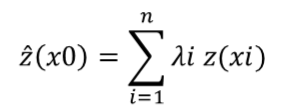Le contexte de l’information géographique s’est largement développé depuis la fin du XXe siècle grâce à l’évolution des outils informatiques. L’apparition conjointe des technologies de l’information et de la communication et la circulation accrue des données, notamment suite à l’avènement de l’internet, font ainsi de la géomatique une discipline nouvelle et indispensable. Celle-ci fait appel à un vocabulaire spécifique et emploie des technologies singulières : les systèmes d’information géographique (SIG). Les SIG sont utilisés pour répondre à des problématiques très variées à travers une approche multidisciplinaire et multithématique, comme la météorologie, les réseaux de transports, le marketing, la sécurité, l’agriculture, aménagement et urbanisme…
Un consensus de définitions montre que les SIG ne peuvent être considérés comme de simples logiciels de traitement de données spatialisées. Parmi ces définitions, celle de Françoise De Blomac illustre bien ce concept :
« Un SIG est un ensemble organisé de matériels informatiques, de logiciels, de données géographiques et de personnels capables de saisir, stocker, mettre à jour, manipuler, analyser et présenter toutes formes d’informations géographiquement référencées » (De Blomac et al., 1994).
Les fonctions des SIG
Plusieurs fonctions peuvent être attribuées à ces systèmes, qui en font des outils complets de connaissance, d’aide à la décision et de communication.
- Création et collecte de données géoréférencées, issues de sources multiples et de formats très divers : numérisation de fonds de cartes ou de photographies aériennes, digitalisation et géocodage de données de terrain, harmonisation spatiale, temporelle et structurelle des données.
- Stockage, organisation et spatialisation de ces informations grâce à un système de gestion de bases de données (SGBD).
- Affichage et superposition de différentes couches d’information géographique sous forme de cartographies pour une visualisation spatialisée des phénomènes terrestres.
- Interrogation, analyse spatiale et/ou statistique pour mettre en évidence les tendances et interactions géographiques entre ces différents phénomènes.
Quels types de données peuvent être intégrés dans un SIG ?
Fernandez-Falcon et al. (1993) estiment à plus de 80 % les informations possédant une référence spatiale. Techniquement, ces données peuvent être de deux natures : les images et les vecteurs.
Les images, également appelées rasters, sont constituées d’une matrice de pixels géoréférencés auxquels sont attribuées des valeurs radiométriques de couleur. Les photographies aériennes et les cartes topographiques sont des exemples de rasters couramment utilisés.
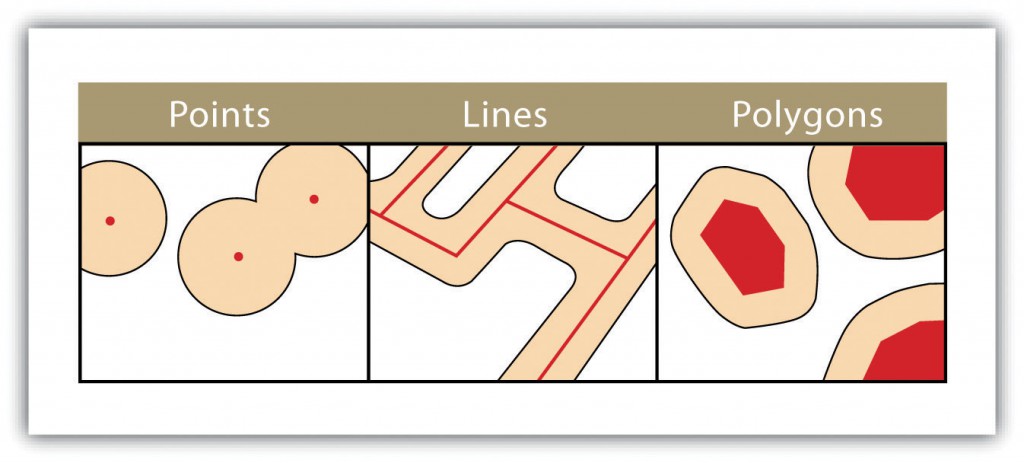
Les données vecteurs sont composées d’objets géographiques de forme élémentaire. Les points sont des coordonnées XY, les lignes sont une succession de points de coordonnées XY et les polygones sont une succession de points de coordonnées XY délimitant une surface fermée.
Toutes ces informations sont représentées sous forme de couches superposables permettant de représenter un phénomène réel.
Les outils de base d’analyse spatiale
Grâce aux SIG, nous disposons d’un grand nombre d’outils d’analyse spatiale pour évaluer les structures et processus géographiques de plusieurs jeux de données. Ces outils se basent notamment sur plusieurs concepts comme la distance, l’interaction spatiale ou la centralité. Dans le champ de la santé environnementale, de puissants outils d’analyse spatiale peuvent être employés.
Le géocodage
Localiser les objets ou les personnes sur Terre, en transformant une adresse postale (référence géographique implicite) en coordonnées spatiales (référence géographique explicite).
⇒ En santé-environnement, le géocodage est utilisé pour localiser les patients à partir de leur adresse de résidence, ou positionner un point de prélèvement de terrain sur la carte.
L’analyse de distances/surfaces
Identifier les objets les plus proches, calculer la superficie d’entités surfaciques, créer des zones tampon.
⇒ En santé-environnement, ces outils peuvent être utilisés pour générer des indicateurs de proximité : calculer le nombre d’industries à risque dans un rayon de 10 kilomètres d’une commune, sélectionner les patients habitant à moins de 300 mètres d’un axe routier majeur, identifier la zone d’influence d’une source d’émissions en polluants en intégrant la direction des vents dominants.
La superposition ou jointure spatiale
Sélectionner des entités en fonction d’une relation spatiale et faire ressortir des indicateurs statistiques en sortie.
⇒ En santé-environnement, la jointure spatiale permet par exemple de calculer la part d’un territoire occupée par des terres cultivées, le nombre et la longueur totale des axes routiers qui traversent une commune, ou agréger des mesures de polluants effectuées au sein d’une même zone (quartier, commune). Ces outils peuvent également être utilisés pour identifier les populations sensibles (crèches, hôpitaux) potentiellement exposées à un danger, comme le risque industriel ou une zone contaminée.
L’analyse de tendance spatiale
Bien que la cartographie aide à apprécier les tendances spatiales d’un phénomène géographique, des modèles spatiaux doivent être utilisés pour comprendre et quantifier ces patterns. Basés sur la statistique inférentielle, ces modèles évaluent le degré de significativité d’une tendance spatiale des données : les entités, ou les valeurs associées aux entités ne constituent pas un modèle spatialement aléatoire.
⇒ En santé-environnement, ces outils peuvent par exemple être utilisés pour identifier des points noirs environnementaux. Il s’agit de zones géographiques fortement polluées et densément peuplées. Un point d’échantillonnage doté d’une valeur élevée en polluant est une information intéressante, mais il ne s’agit pas forcément d’un point chaud statistiquement significatif. Un point chaud est en effet considéré lorsqu’une entité a une valeur élevée et qu’elle est entourée d’autres entités également dotées de valeurs élevées. La statistique de Getis-Ord Gi* identifie alors l’agrégation spatiale statistiquement significative de valeurs élevées (points chauds) et de valeurs faibles (points froids).
Les outils d’épidémiologie spatiale
Pour cartographier les données de santé, les patients sont d’abord géocodés à partir de leur adresse de résidence. Les données sont ensuite agrégées à l’unité spatiale la plus pertinente pour l’étude (région, cantons, communes, quartiers par exemple).
La cartographie des maladies
La cartographie d’incidence de maladie est basée sur le calcul d’indicateurs agrégés au sein d’unités géographique, représentant la proportion de malades au sein de la population : le nombre de cas pour 100 000 habitants par commune par exemple. Ces indicateurs d’incidence sont considérés comme très « instables » en cas de faibles effectifs de population ou de maladies rares. Le résultat cartographique est dans ce cas bruité et difficilement interprétable en raison de la forte hétérogénéité des densités de population au sein du territoire. De plus, représenter ces indicateurs de manière brute sur une carte implique de considérer les risques indépendamment d’une unité géographique à l’autre, sans tenir compte de l’information fournie par les unités voisines. La fréquence d’une maladie dans une zone géographique n’est pourtant pas indépendante de celle des zones voisines (phénomène d’autocorrélation spatiale).
« Everything is related to everything else, but near things are more related than far things. » (Waldo Tobler, 1970)
Afin de présenter des cartographies fiables de répartition spatiale de la fréquence des maladies, ce phénomène de ressemblance est utilisé pour réduire la variance des estimations de risque, à travers des modèles de lissage de ces indicateurs (Clayton & Kaldor, 1987). Ces modèles ont été développés pour mieux estimer la structure spatiale sous-jacente de l’incidence et lisser le bruit observé dans les zones présentant un faible nombre de cas, en partageant l’information apportée par les unités voisines (Elliott & Wartenberg, 2004).
Plusieurs modèles de lissage sont recensés dans la littérature (Auchincloss et al., 2012). Parmi les plus utilisés pour estimer les risques de maladies rares figurent les modèles hiérarchiques bayésiens, notamment celui de Besag, York et Mollié (1991), qui a l’avantage d’identifier simultanément une structure spatiale globale et locale.
La détection d’agrégats (clusters)
Les techniques de cartographie des maladies sont employées pour évaluer l’hétérogénéité spatiale d’incidence des évènements de santé. Bien qu’elles soient indispensables pour décrire la distribution géographique, elles ne permettent pas de détecter des zones d’incidence atypique, appelées clusters, et d’évaluer leur significativité. Un cluster est une concentration de cas « anormalement » faible ou élevée par rapport à celle attendue sur la zone. Pour identifier ces zones géographiques atypiques, les méthodes de balayage spatial peuvent être employées, telle que la statistique de scan.
Développée par Martin Kulldorff dans la fin des années 1990, la statistique de scan détecte des clusters d’évènements spatiaux, temporels et spatio-temporels, sans biais de présélection. Cette détection peut être validée par un test de significativité pour chacun des clusters et ajustée par des facteurs confondants, comme l’âge et le sexe (Kulldorff 1997 ; Kulldorff et al. 1998).
Le principe de cette statistique se déroule en deux étapes. Dans une première phase de détection, une fenêtre de forme et de taille variable balaye la zone d’étude (dans l’espace et/ou le temps) pour comptabiliser les évènements observés à partir de chaque centroïde d’unité géographique (centre géographique représenté par des coordonnées XY). Pour chacun des emplacements et tailles de fenêtre, une fonction de probabilité (le risque relatif : RR) est alors calculée en considérant la distribution des cas de maladie selon une loi de Poisson. Le RR dépend à la fois du nombre de cas observés à l’intérieur de la fenêtre de scan et du nombre de cas observés à l’extérieur.
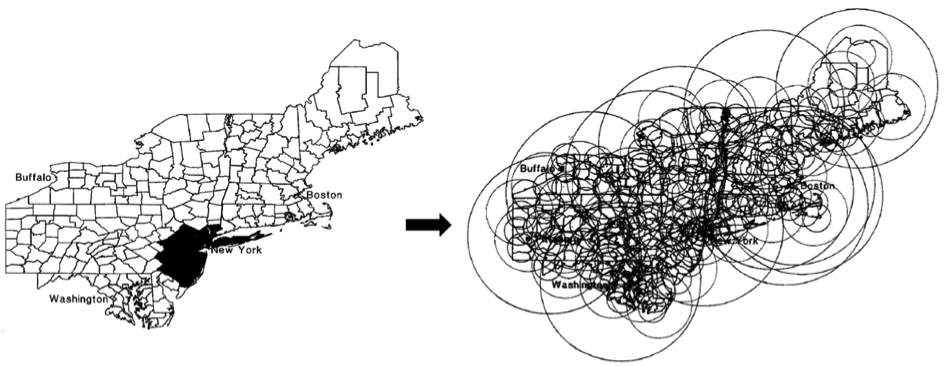
Un petit échantillon des nombreuses fenêtres de scan utilisées par SaTScanTM (modifié à partir de Kulldorff, 1999)
La deuxième phase est ensuite celle de l’inférence statistique afin de déterminer le niveau de significativité d’un cluster. L’hypothèse nulle correspond à l’absence de cluster (le risque est homogène et constant sur l’ensemble de la zone et/ou de la période d’étude) et l’hypothèse alternative à la présence d’au moins un cluster atypique (le risque est différent à l’intérieur de la fenêtre par rapport à l’extérieur de la fenêtre).
Les premières applications épidémiologiques de cette statistique furent consacrées à la leucémie infantile et à la mortalité par cancer du sein dans la région de New-York (Hjalmars et al. 1996; Kulldorff et al. 1997). Cette méthode a ensuite largement été appliquée à travers le monde. Le site internet proposant le téléchargement gratuit du logiciel recense par exemple plus de 200 publications concernant 40 thématiques différentes, comme la criminologie, la botanique ou encore l’archéologie (SaTScan).
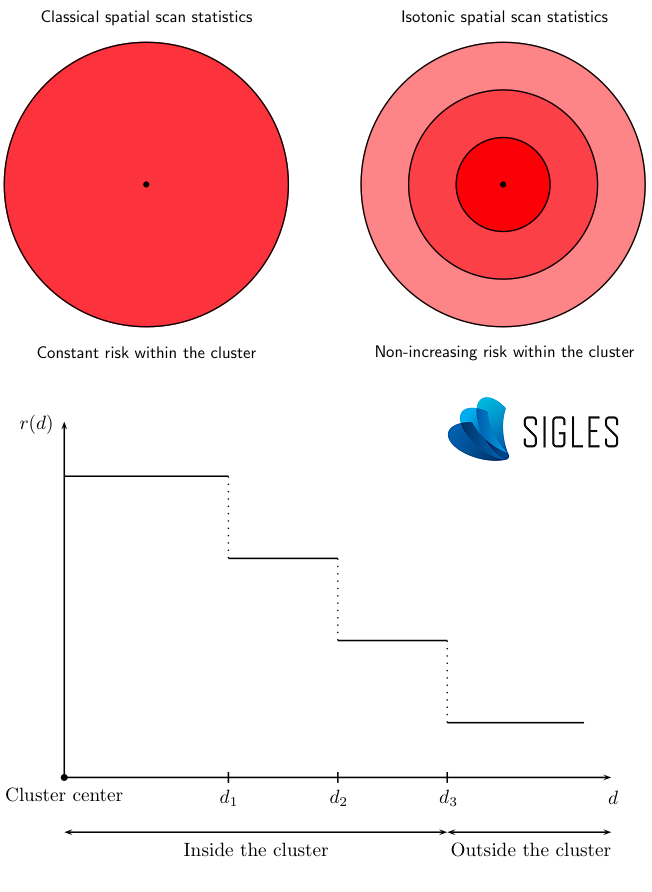
Une version plus évoluée de la statistique de scan permet d’estimer des risques non homogènes au sein de chaque cluster détecté (Kulldorff, 1999). En effet, la version isotonique de SaTScanTM peut déterminer plusieurs niveaux de risque à l’intérieur d’un même cluster grâce à une fonction de régression isotonique décroissante en fonction de la distance au centre du cluster. Cette fonction apporte une information supplémentaire, notamment pour l’identification précise des zones atypiques d’incidence (épicentre) dans le cas de clusters de grande taille.
L’interpolation spatiale
La plupart des bases de données issues de la surveillance physico-chimique et biologique de l’environnement peuvent constituer des informations géostatistiques. Cette information peut être définie par des mesures quantitatives réalisées au niveau d’un échantillon de points géolocalisés dans l’espace. La logistique et le coût élevé des prélèvements et d’analyse des échantillons nécessitent la mise en place de plans d’échantillonnage. La répartition des échantillons dans l’espace peut alors s’avérer hétérogène sur la zone étudiée. Des méthodes d’analyse spatiale ont été développées afin de générer des représentations cartographiques globales de ces indicateurs de qualité des milieux environnementaux et évaluer les principales tendances du phénomène observé (Ripley, 1981 ; Cressie, 1993). L’interpolation spatiale est une méthode d’estimation statistique de données spatialisées. Son principe est qu’à partir d’observations ponctuelles mesurées et géoréférencées, elle fournit la valeur la plus probable du paramètre observé (appelé variable régionalisée) en tout point du domaine spatial étudié (Hengl, 2007). Le résultat est une production cartographique d’estimations au niveau de chaque point d’une grille régulière recouvrant la zone d’étude.
En santé-environnement, l’interpolation spatiale peut être utilisée pour générer des proxys d’exposition aux polluants, notamment pour prédire le niveau de contamination de l’environnement au niveau d’une zone géographique globale (un quartier, une commune) ou même au niveau des lieux d’habitation des patients.
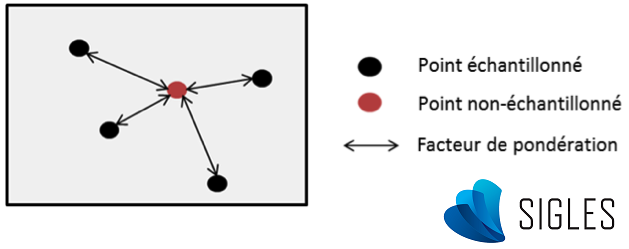
Principe général de l’interpolation spatiale
Pour prévoir la valeur d’un point non échantillonné à partir de plusieurs points d’observation, la formule mathématique simplifiée de l’interpolation spatiale peut être assimilée à une moyenne arithmétique pondérée des valeurs observées (Li & Heap, 2014) :
où ^z est la valeur estimée de la variable aléatoire au point d’intérêt x0, z est la valeur observée au point d’échantillon xi , λi est le facteur de pondération attribué à ce point d’échantillon et n le nombre d’échantillons utilisés pour l’estimation.
Deux grandes approches
Les méthodes d’interpolation spatiale peuvent être classées selon deux grandes approches : l’approche déterministe et l’approche géostatistique. La principale différence de ces méthodes est la manière dont va être attribué le poids de chaque point d’observation dans le calcul d’estimation.
Les méthodes déterministes d’interpolation reposent essentiellement sur des propriétés mathématiques et géométriques, sans tenir compte de la structure spatiale du phénomène. La pondération est uniquement fonction de la distance euclidienne entre le site d’observation et le site de prédiction. Les sites d’observation les plus proches ont ainsi une plus grande influence dans le calcul, alors qu’un poids faible (ou nul) est généralement attribué aux sites les plus éloignés.
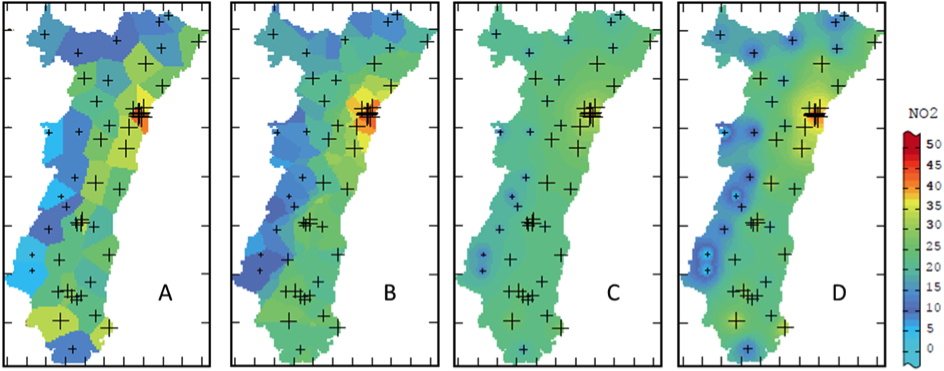
Estimation de la concentration en dioxyde d’azote en Alsace par différentes méthodes déterministes (A) plus proche voisin, (B) moyenne mobile, (C) inverse des distances et (D) inverse des distances au carré (modifié à partir de Lemarchand & Jeannée, 2009)
Les méthodes probabilistes (ou stochastiques) d’interpolation sont appelées méthodes géostatistiques, puisqu’elles découlent directement de l’analyse géostatistique des données d’observation et incorporent le concept du phénomène naturel (Cressie, 1993 ; Goovaerts, 1997). En plus d’une structure déterministe, elles incluent des notions d’erreurs aléatoires pour représenter le comportement spatial d’un phénomène naturel (Hengl, 2007). Parmi les méthodes géostatistiques, le krigeage est considérée comme la méthode optimale d’interpolation pour les phénomènes environnementaux, puisqu’il prend en considération la structure de dépendance spatiale des données afin de minimiser l’erreur de prédiction. En se basant sur les données d’observation et la modélisation d’un variogramme expérimental, le krigeage va attribuer un poids à chacun des sites mesurés à partir de la covariance entre ces points, en fonction de la distance qui les sépare. Ainsi, la pondération est une fonction de plusieurs composantes : la distance entre la valeur observée et la valeur à estimer (comme pour l’approche déterministe), la structure spatiale de l’échantillonnage (présence de vides ou de clusters de points mesurés) et le comportement spatial du phénomène observé (variabilité spatiale brutale ou lente, direction privilégiée, etc.).
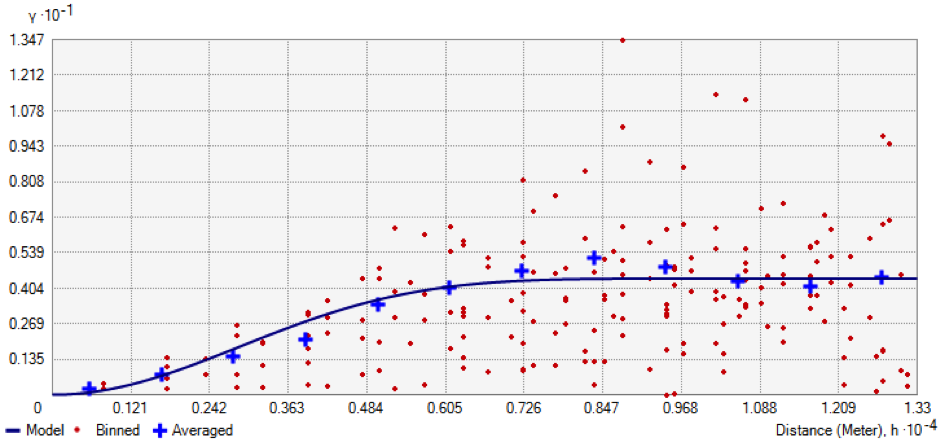
Exemple de variogramme expérimental représentant l’écart de valeur entre les paires de points en fonction de la distance qui les sépare (logiciel ArcGIS®)
Les méthodes de krigeage proposent également d’autres avantages. Il est par exemple possible de définir un poids plus ou moins important en fonction d’une direction (phénomène d’anisotropie). Cela permet par exemple de tenir compte de l’origine des vents dominants dans le cadre du suivi d’un panache de cheminée, ou le sens d’écoulement d’une rivière pour le suivi des sédiments (Merwade, 2009). Un autre avantage de certaines méthodes de krigeage (le co-krigeage) est l’intégration de variables auxiliaires, évoluant de la même manière dans l’espace que la variable régionalisée, pour améliorer le calcul du variogramme (Lemarchand & Jeannée, 2009). Mais la forte plus-value de cette méthode par rapport aux autres est le calcul d’une erreur probable d’estimation associée à chaque point non échantillonné. Cette erreur de prédiction est globalement plus élevée au niveau des zones pauvres en échantillons et à proximité des points observés ayant des valeurs extrêmes. Un phénomène présentant une variabilité élevée dans l’espace entraine des niveaux d’incertitudes plus importants.
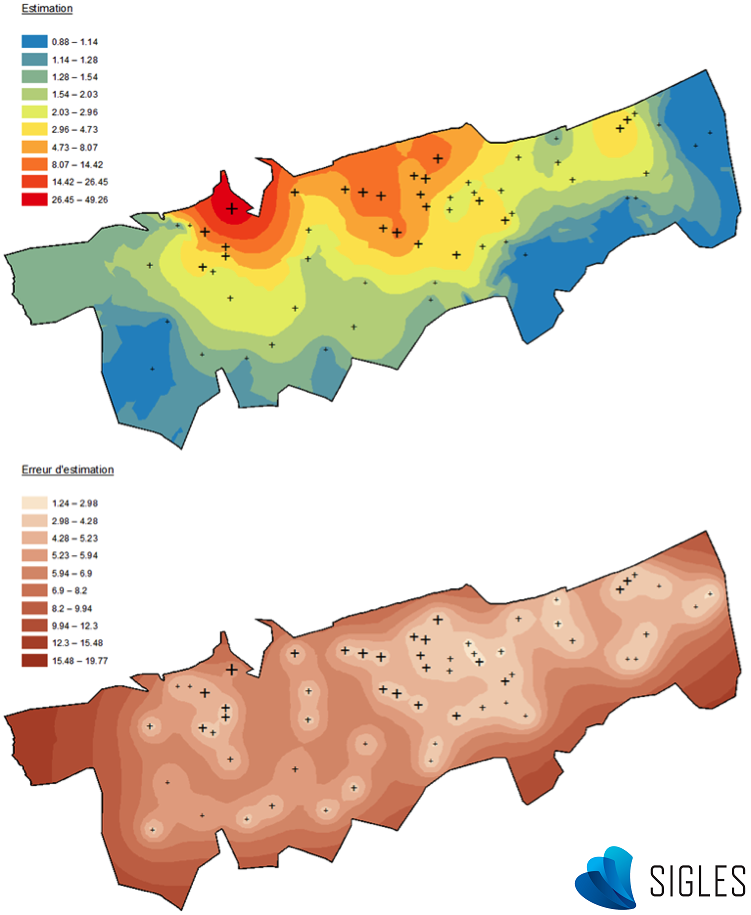
Résultats du krigeage (logiciel ArcGIS®). La cartographie de l’estimation de la variable aléatoire (en haut) et la cartographie de l’erreur d’estimation (en bas)
Références bibliographiques
Auchincloss AH, Gebreab SY, Mair C, Diez Roux AV. 2012. A review of spatial methods in epidemiology, 2000-2010. Annu Rev Public Health, 33: 107-122.
Besag J, York J, Mollié A. 1991. Bayesian image restoration, with two applications in spatial statistics (with Discussion). Annals of the Institute of Statistical Mathematics, 43(1): 1-59.
Campbell J & Shin M. 2011. Essentials to Geographic Information Systems. Flat World Knowledge, Inc. 171p.
Clayton D & Kaldor J. 1987. Empirical Bayes estimates of age-standardized relative risks for use in disease mapping. Biometrics, 43: 671-681.
Cressie NA. 1993. Statistics for Spatial Data (revised edition). John Wiley & Sons, Inc., New York.
De Blomac F, Gal R, Hubert M, Richard D, Tourret C. 1994. Arc/Info, concepts et applications en géomatique. Paris, Hermès, 256 p.
Elliott P & Wartenberg D. 2004. Spatial Epidemiology: Current Approaches and Future Challenges. Environmental Health Perspectives, Vol 112: 998-1006.
Fernandez-Falcon E, Strittholt JR, Alobaida AI, Schmidley RW, Bossler JD, Ramirez JR. 1993. A Review of Digital Geographic Information Standards for the State/Local User. URISA Journal, Vol 5 (2): 21-27.
Goovaerts P. 1997. Geostatistics for Natural Resources Evaluation. Oxford University Press, New York.
Hengl T. 2007. A Practical Guide to Geostatistical Mapping of Environmental Variables. Office for Official Publication of the European Communities, Luxembourg, 143p.
Hjalmars U, Kulldorff M, Gustafsson G, Nagarwalla N. 1996. Childhood leukemia in Sweden: Using GIS and a spatial scan statistic for cluster detection. Statistics in Medicine, 15: 707-715.
Kulldorff M. 1997. A spatial scan statistic. Communications in statistics: theory and methods, 26 (6): 1481–1496.
Kulldorff M, Feuer EJ, Miller BA, Freedman LS. 1997. Breast cancer in northeastern United States: A geographical analysis. American Journal of Epidemiology, 146: 161-170.
Kulldorff M, Athas WF, Feurer EJ, Miller BA, Key CR. 1998. Evaluating cluster alarms: a space-time scan statistic and brain cancer in Los Alamos, New Mexico. Am J Public Health, 88 (9): 1377–1380.
Kulldorff M. 1999. An isotonic spatial scan statistic for geographical disease surveillance. Journal of the National Institute of Public Health, 48: 94–101.
Lemarchand O, Jeannée N. 2009. Méthodes de cartographie et approche géostatistique – La cartographie de la pollution au dioxyde d’azote en Alsace. Cahier des thèmes transversaux ArScAn, 9: 203-214.
Li J & Heap AD. 2014. Spatial interpolation methods applied in the environmental sciences: a review. Environmental Modelling & Software, 53: 173-189.
Merwade V. 2009. Effect of spatial trends on interpolation of river bathymetry. Journal of Hydrology, 371: 169–181.
Rican S. 2007. Représentation cartographique des données sanitaires. Séminaire ORS Île de France « De la mesure des expositions à l’évaluation des conséquences pour la santé : le traitement spatialisé des données ». Paris, 7 septembre 2007. Communication orale.
Ripley BD. 1981. Spatial Statistics. New York: Wiley.
Tobler W. 1970. A Computer Movie Simulating Urban Growth in the Detroit Region. Economic Geography, 46: 234–40.